[Gold V] 1, 2, 3 더하기 4 - 15989
성능 요약
메모리: 69100 KB, 시간: 12 ms
분류
다이나믹 프로그래밍
제출 일자
2024년 2월 7일 20:38:29
문제 설명
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 4가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다. 합을 이루고 있는 수의 순서만 다른 것은 같은 것으로 친다.
- 1+1+1+1
- 2+1+1 (1+1+2, 1+2+1)
- 2+2
- 1+3 (3+1)
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 10,000보다 작거나 같다.
출력
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
풀이
해당 문제의 유형이 DP인 것을 알고 규칙을 찾아보았습니다. 우선 N을 나타내는 방법의 수를 dp로 정의하고 경우의 수를 다음과 같이 나눴습니다.
1) (N-3) + 3
2) (N-2) + 2
3) (N-1) + 1
하지만 해당 경우에선 겹치는 부분이 발생할 것이라고 생각하여 겹치는 부분을 제거해주고자 하였습니다.
직접 확인해보기 위해 구해보았습니다.
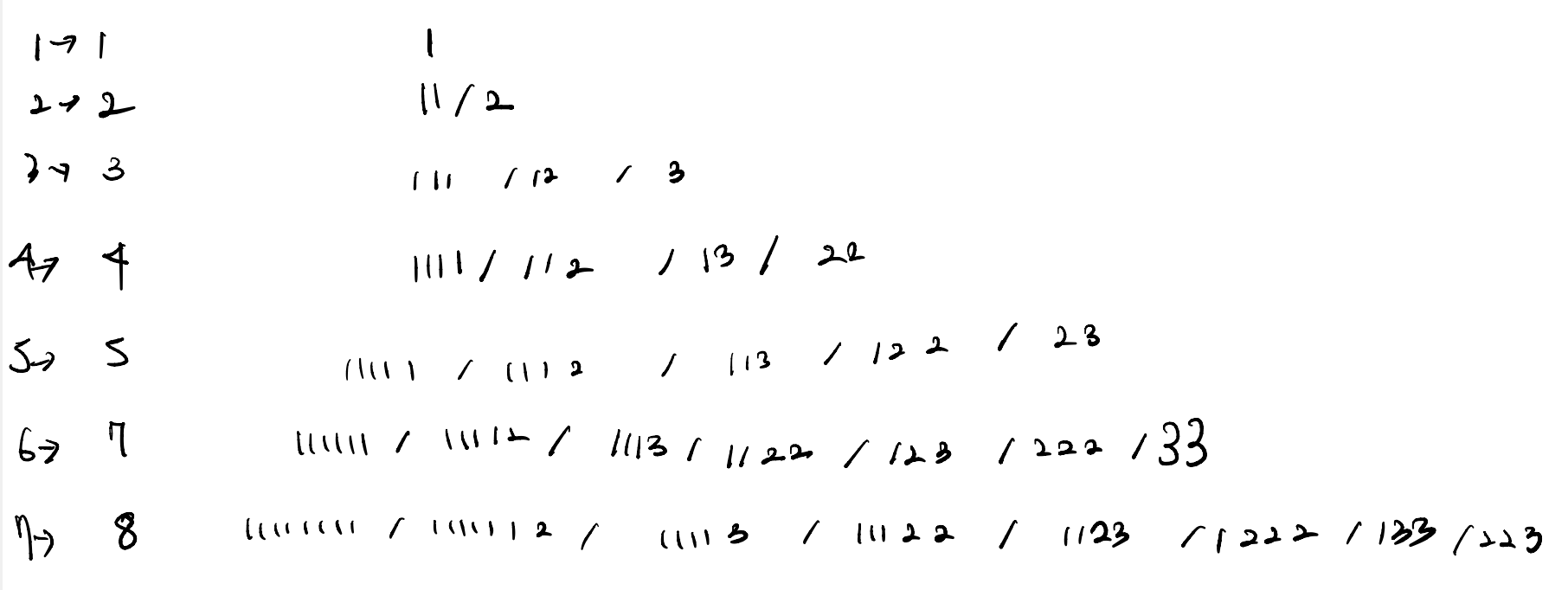
뭔가 와닿지가 않아 5, 6인 경우에서 확인을 해보았습니다.

위 식을 보니 값은 맞지는 않지만 dp[N] = dp[N-1] + dp[N -2] - dp[N-3]을 하면 개수가 얼추 맞긴한데, 6, 9인 경우에선 맞지 않음을 확인하였습니다. 위 값들은 3의 배수로, 만약 3의 배수의 값이 오게 되면 3의 배수로만 만들 수 있는 경우가 있기 때문에, 1가지의 경우의 수를 더해주어야 했습니다.
다른 값들 또한 이 값과 일치하여 시도해보았더니 답이 맞았습니다. 어떠한 규칙을 통해 위와 같이 나온 지는 정확하진 않지만,, 위와 같은 식으로 dp를 구성하면 정답을 구할 수 있었습니다.
다음은 코드입니다.
let n = Int(readLine()!)!
var dp = Array(repeating: 0, count: 10001)
(dp[1], dp[2], dp[3]) = (1, 2, 3)
for i in 4...10000 {
dp[i] = dp[i - 1] + dp[i - 2] - dp[i - 3]
if i % 3 == 0 {
dp[i] += 1
}
}
for _ in 0..<n {
print(dp[Int(readLine()!)!])
}'PS > BOJ' 카테고리의 다른 글
| [백준(BOJ)] 2688 줄어들지 않아 - 스위프트 (Swift) (0) | 2024.02.18 |
|---|---|
| [백준(BOJ)] 1904 01타일 - 스위프트 (Swift) (0) | 2024.02.18 |
| [백준(BOJ)] 1431 시리얼 번호 - 스위프트 (Swift) (0) | 2024.02.18 |
| [백준(BOJ)] 11727 2×n 타일링 2 - 스위프트 (Swift) (0) | 2024.02.18 |
| [백준(BOJ)] 16194 카드 구매하기 2 - 스위프트 (Swift) (0) | 2024.02.18 |
