[알고리즘] LCS

LCS

LCS란 보통 최장 공통 부분수열(Longest Common Subsequence)을 의미하지만,

최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.

 

여기에서 부분수열(Subsequence)과 문자열(Substring)의 차이는 문자열이 연속적인지 아닌지에 따라 달라지는데요,

연속적이라면 문자열(Substring)이고, 비연속적이면 부분수열(Subsequence)입니다.

 

다음과 같은 예시가 있다고 가정해봅시다.

 

[AUTABBEHNSAAB, BCUAMEFKAJNAAB]

위 예시에서 AAB는 연속적이기 때문에 문자열이라고 할 수 있고,

UAENAAB는 비연속적이기 때문에 부분 수열이라고 할 수 있습니다.

 

위에서 말한 두 가지의 LCS를 구현하는 방법에 대해 알아보겠습니다.

 

최장 공통 문자열(Longest Common Substring)

최장 공통 문자열이 더 쉽기도 하고, 부분 수열을 구할 때 필요하기 때문에 최장 공통 문자열에 대해 먼저 알아보겠습니다.

if i == 0 || j == 0 {  // 초기값 설정
    LCS[i][j] = 0
} else if string_A[i] == string_B[j] {
    LCS[i][j] = LCS[i - 1][j - 1] + 1
} else {
    LCS[i][j] = 0
}

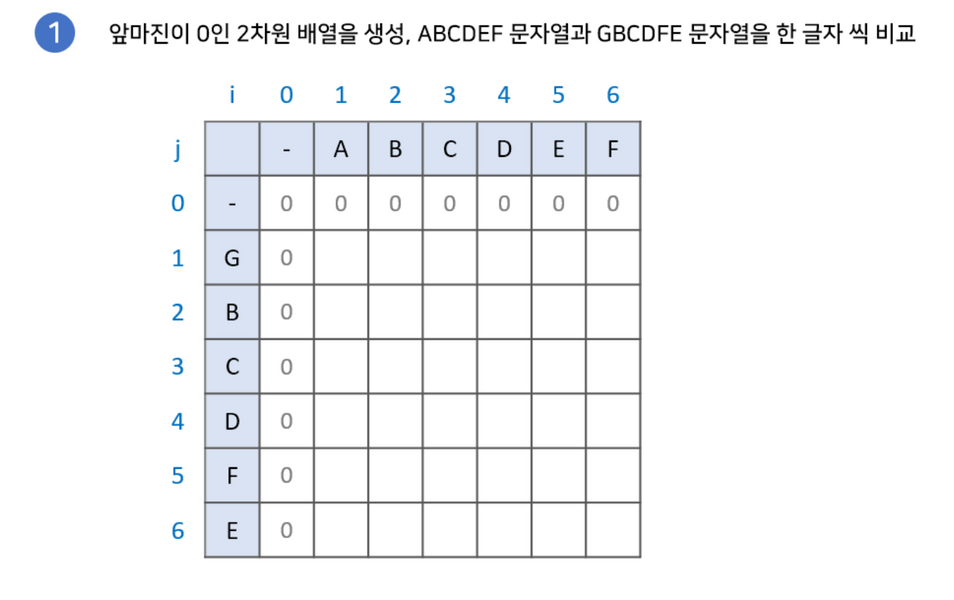
우선 2차원 배열(LCS)을 사용하여 연속적인 문자의 개수를 구할 것입니다.

 

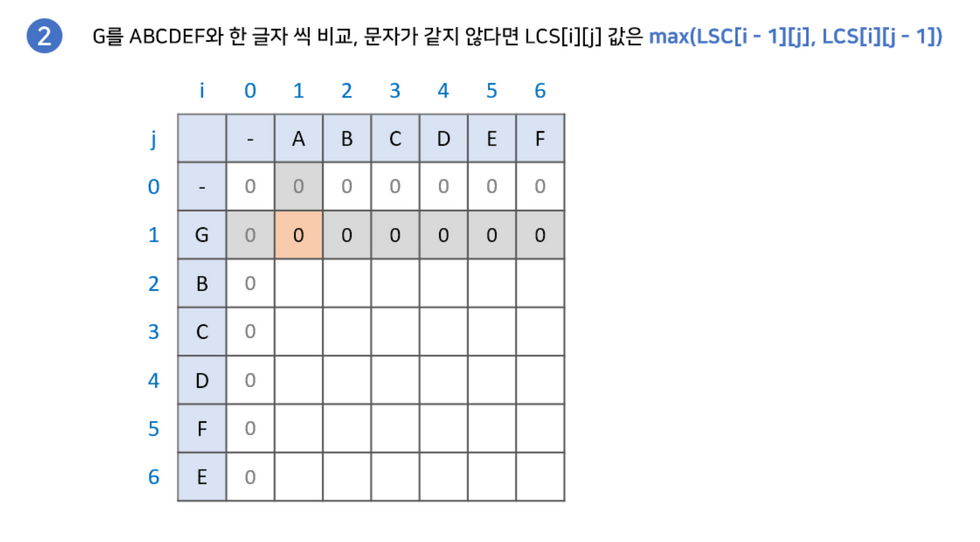
1. 문자열 A와 B를 비교합니다.
2. 만약 두 문자가 같다면 LCS[i][j]에 = LCS[i-1][j-1] + 1을 해줍니다.
3. 만약 다르다면 LCS[i][j]에 0을 대입합니다.

위 식을 반복하게 된다면 최장 공통 문자열의 문자 개수를 얻을 수 있습니다.

 

구현과정에 대해 그림으로 설명한 글이 있어 해당 예시를 이용하겠습니다.

 

 

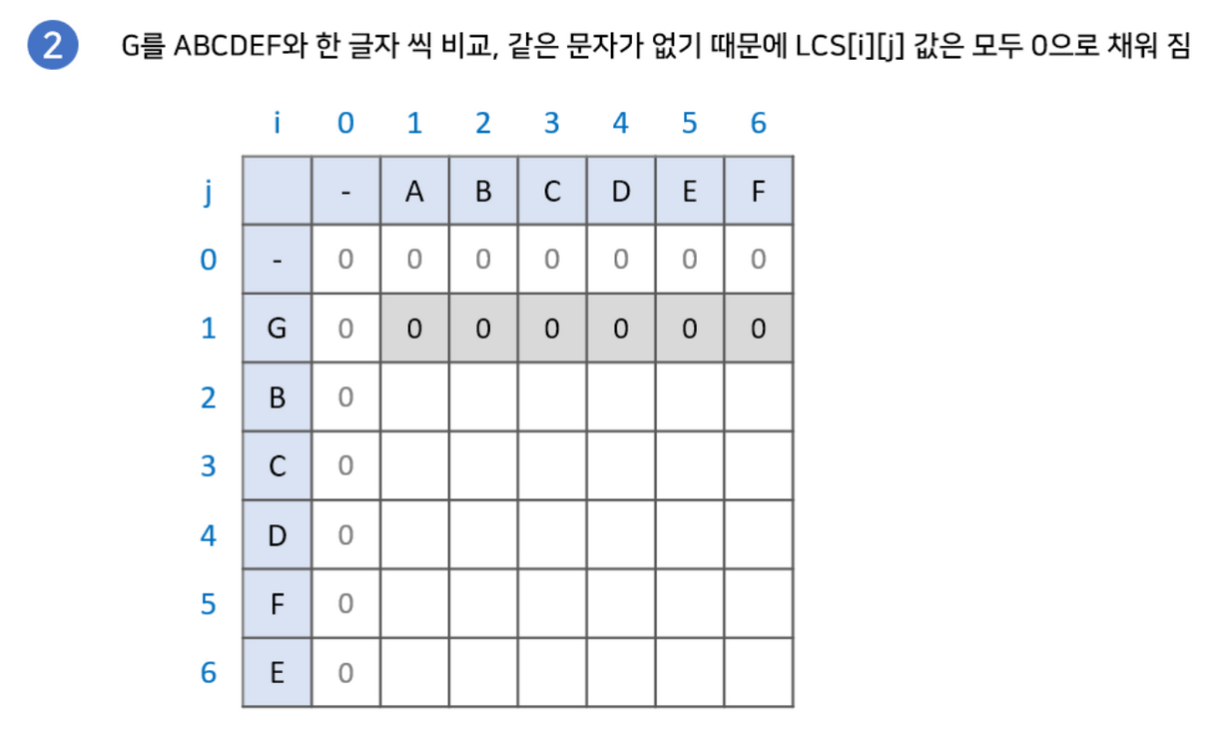
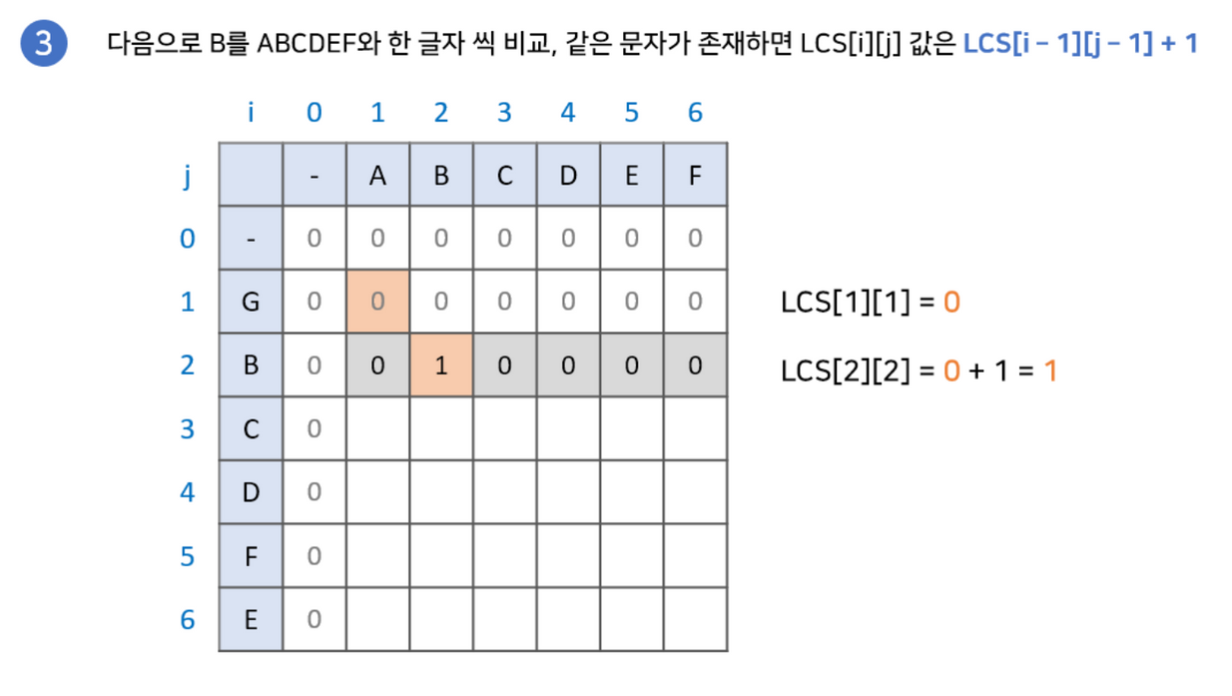
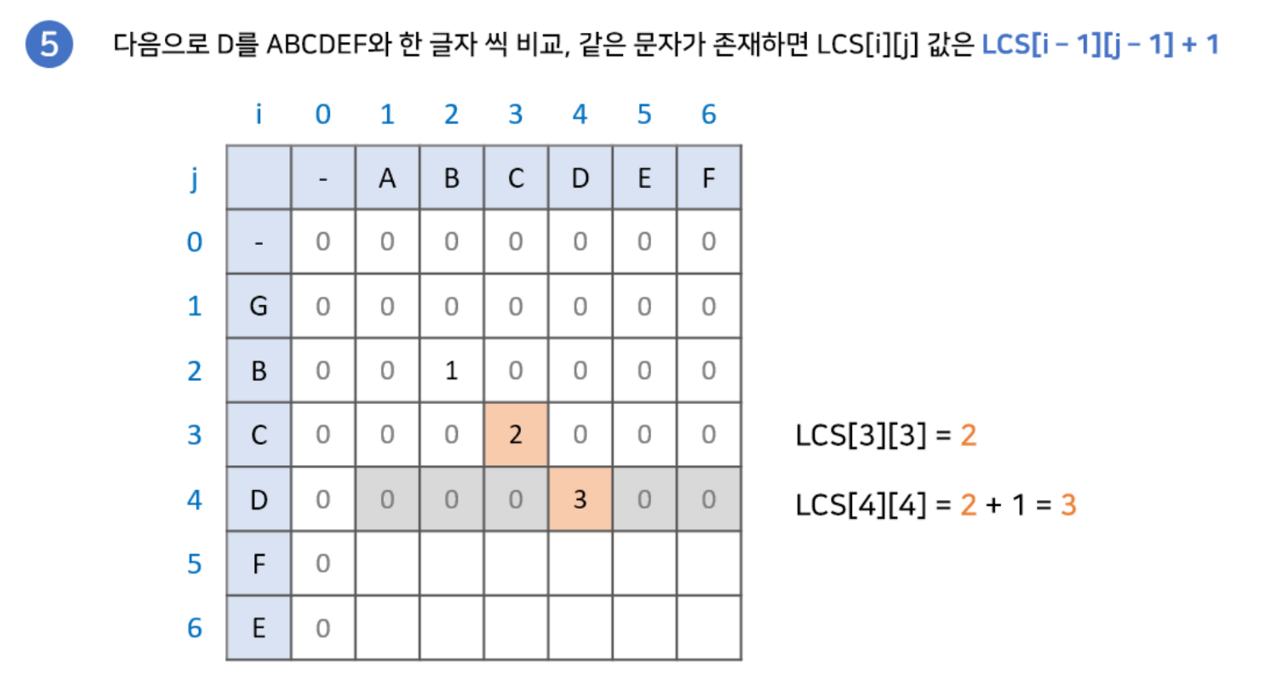
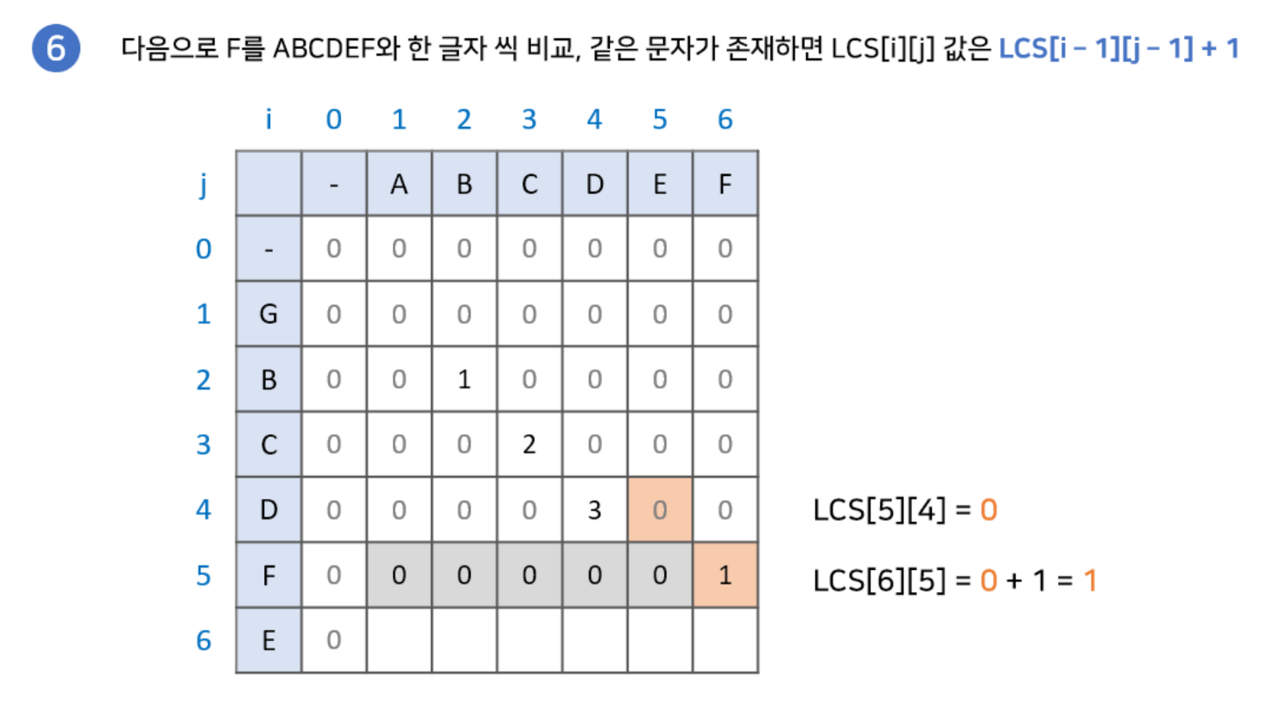
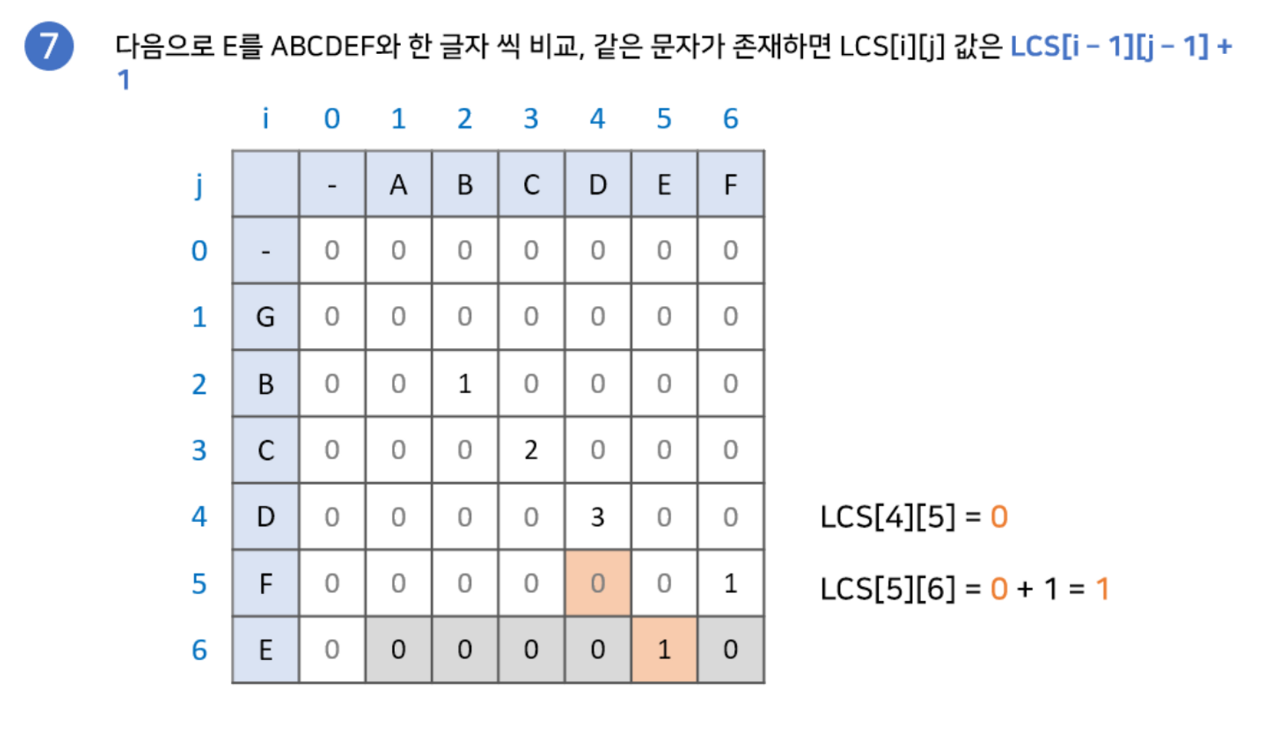
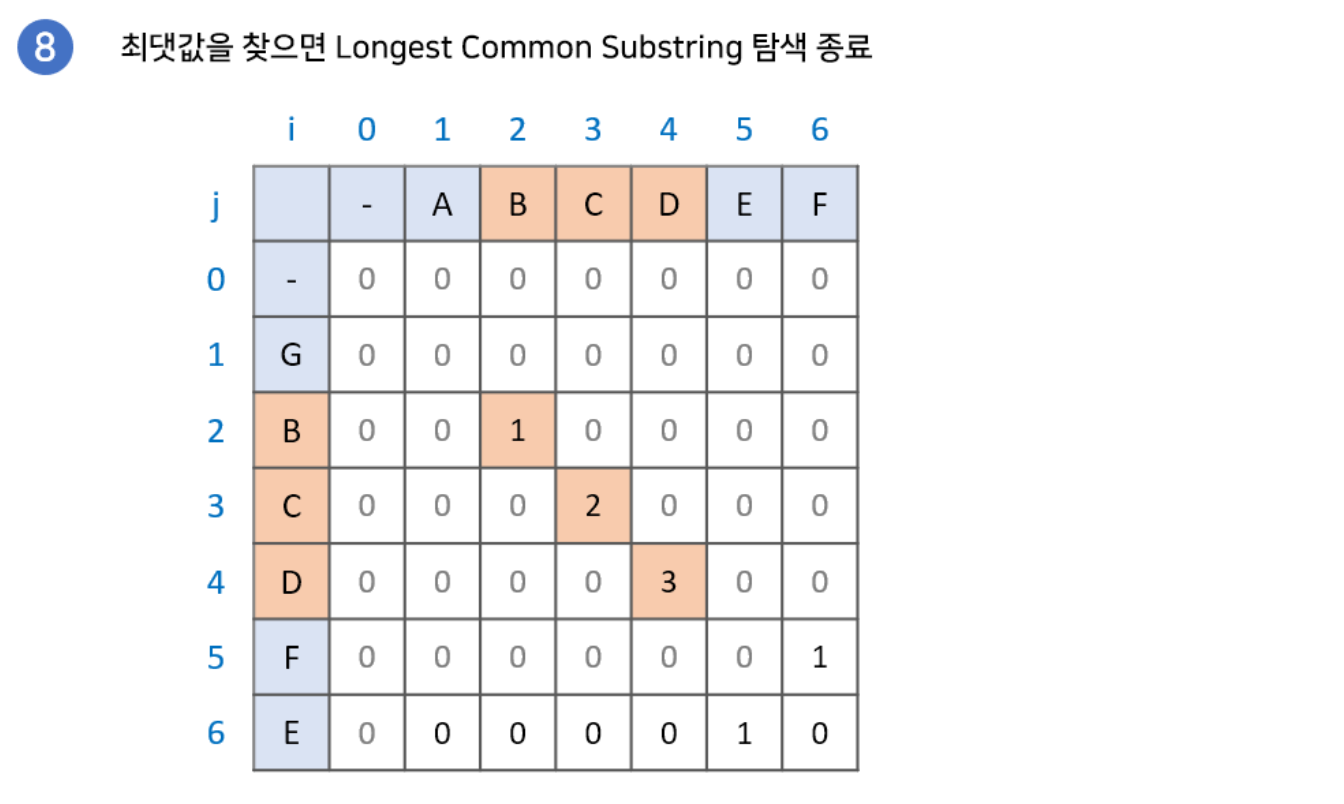
최장 공통 부분 수열(Longest Common Subsequence)

다음은 최장 공통 부분 수열에 대해 알아보겠습니다.

if i == 0 || j == 0 {  // 초기값 설정
    LCS[i][j] = 0
} else if string_A[i] == string_B[j] {
    LCS[i][j] = LCS[i - 1][j - 1] + 1
} else {
    LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1])
}

위 식은 LCS의 최장 길이를 구하는 식입니다.

부분 수열도 2차원 배열로 설정하고 검사합니다.

1. 두 가지의 문자열을 비교합니다.
2. 두 문자가 같다면 LCS[i][j]에 LCS[i-1][j-1] + 1을 해줍니다.
3. 만약 다르다면 LCS[i-1][j]와 LCS[i][j-1] 중에 큰 값을 표시합니다.

문자열과 다른 부분 수열의 차이점은 문자들이 연속되지 않아도 된다는 점입니다.

[i-1][j]와 [i][j-1] 중의 최대값을 표시하는 것은 이전의 과정에서 가장 긴 부분 수열을 저장하기 위함입니다.

 

다음은 구현 과정입니다.

 

 

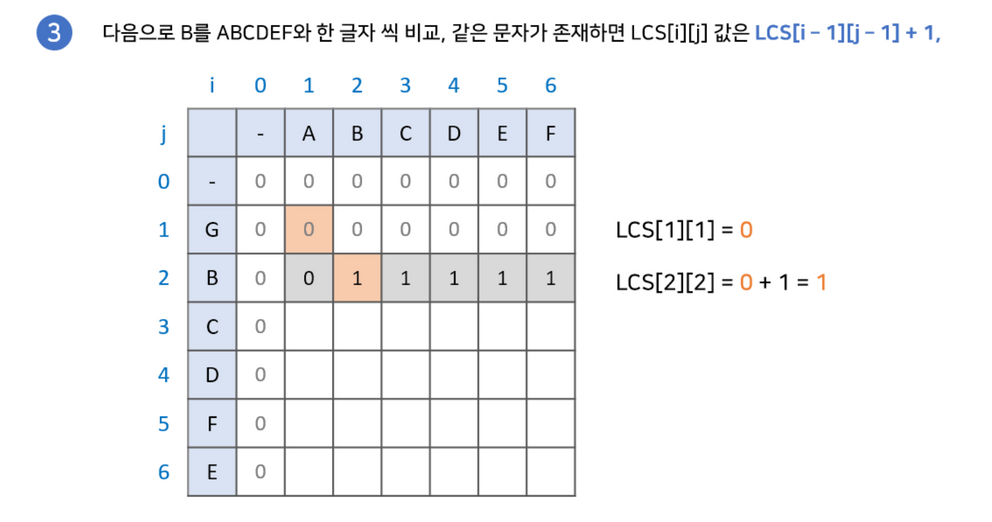
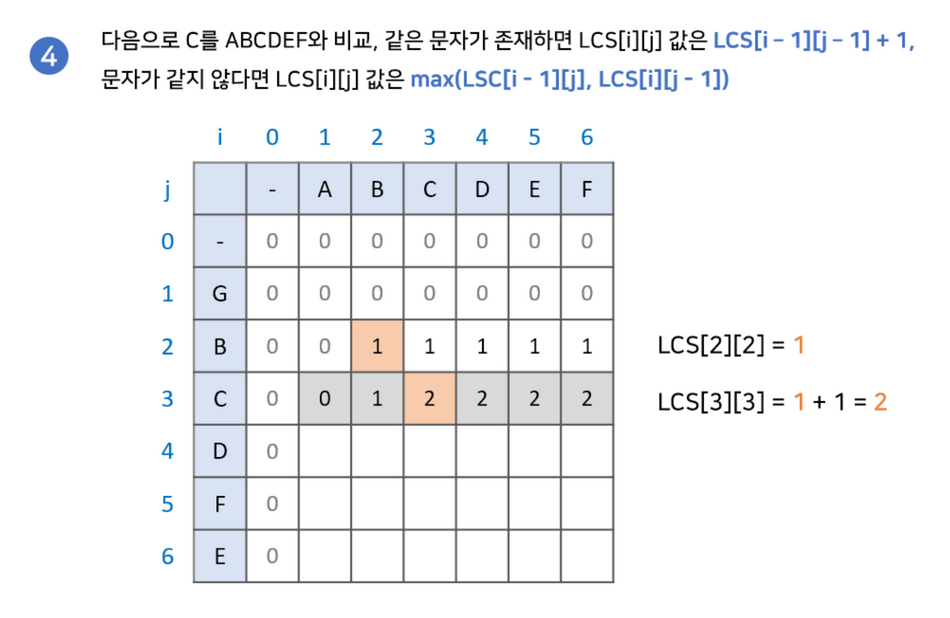
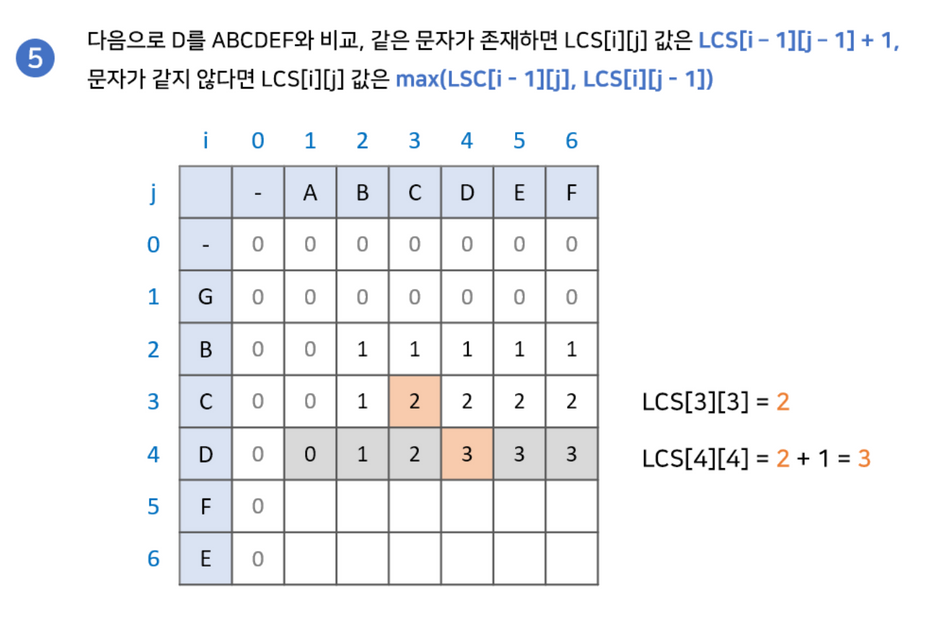
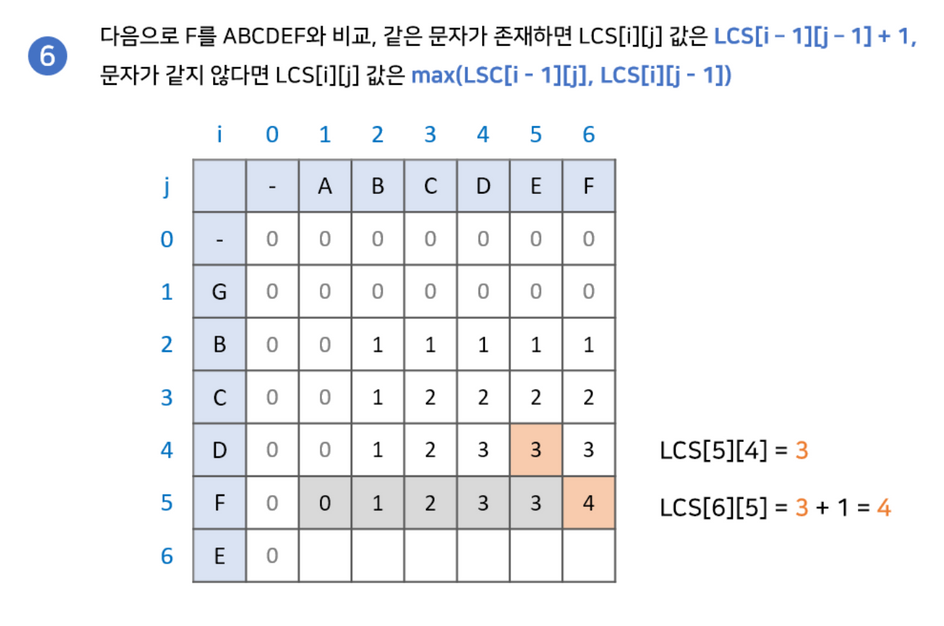
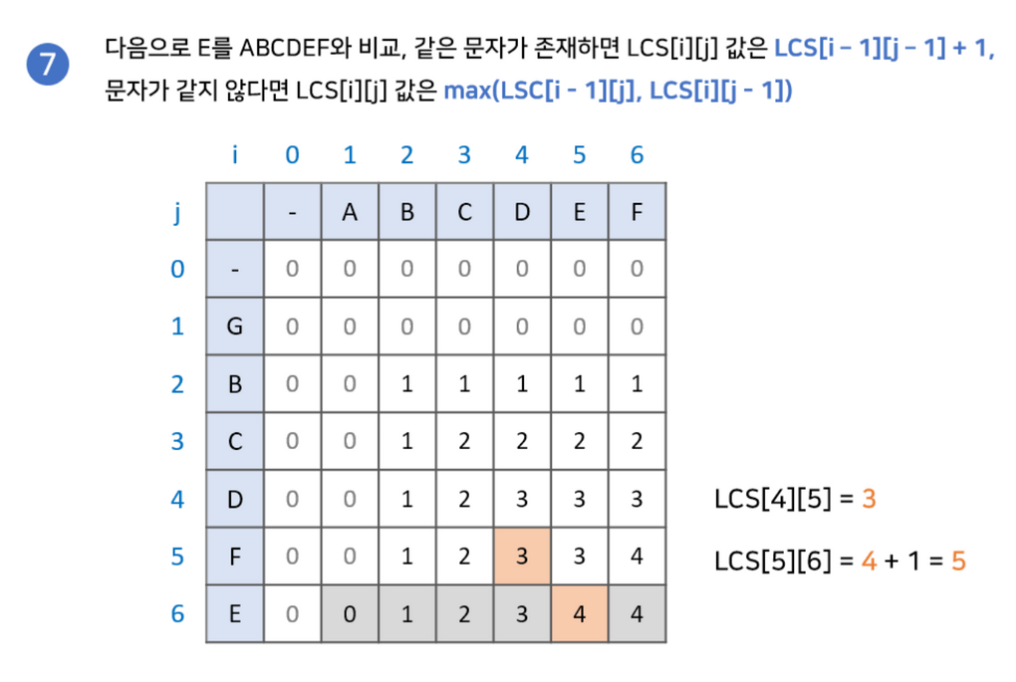
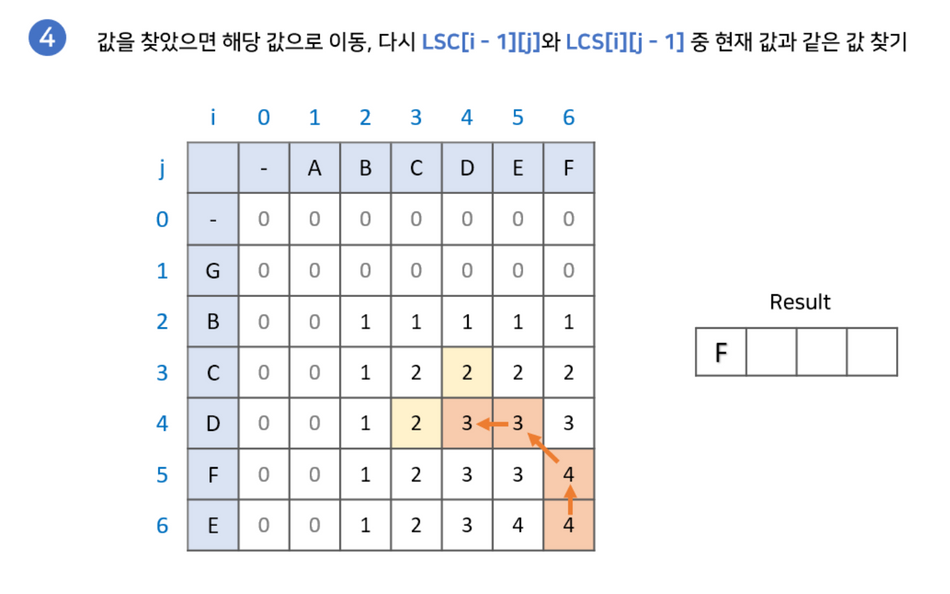
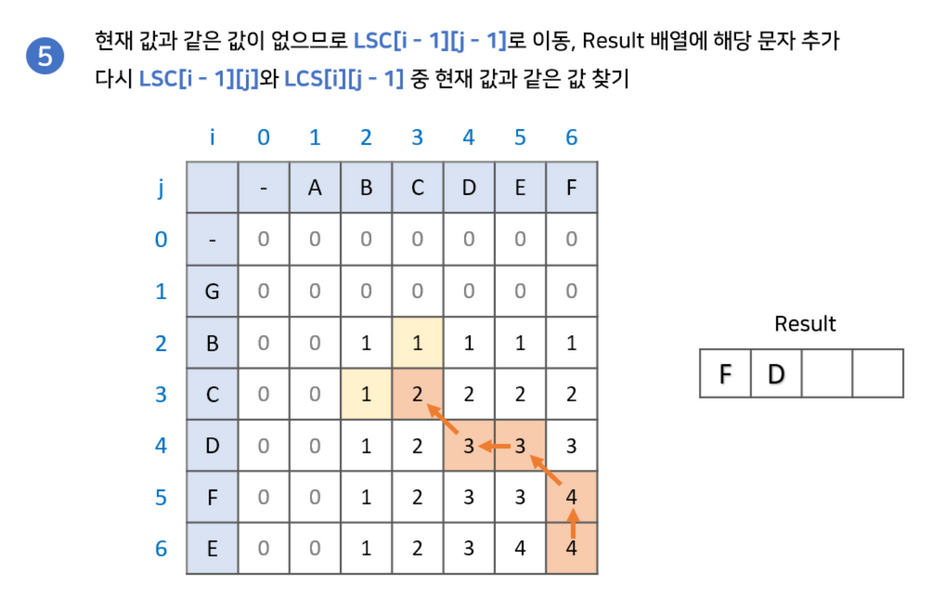
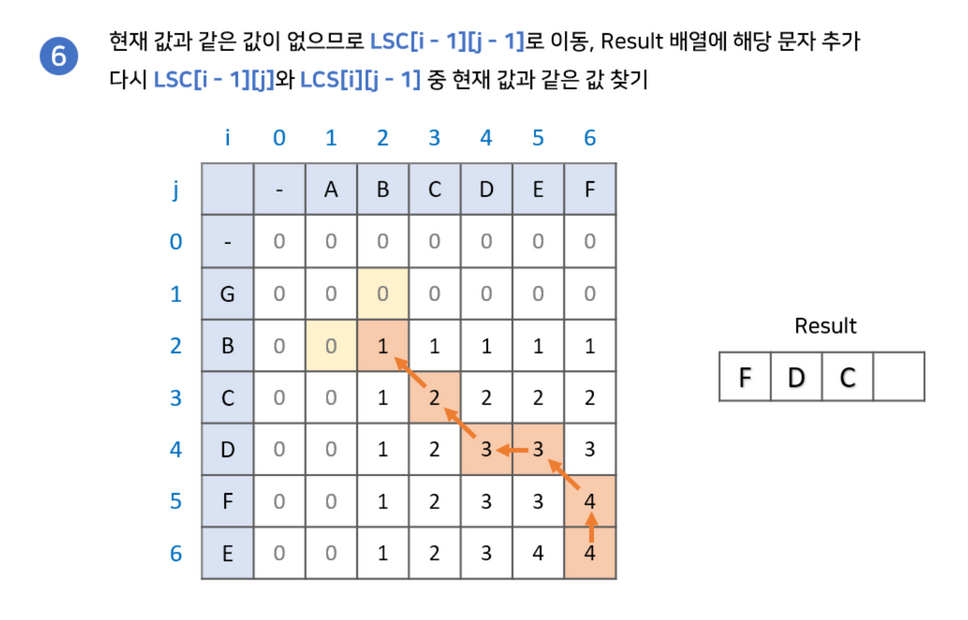
최장 공통 부분 수열 찾기

부분 수열을 찾기 위해서 다음과 같은 과정이 필요합니다.

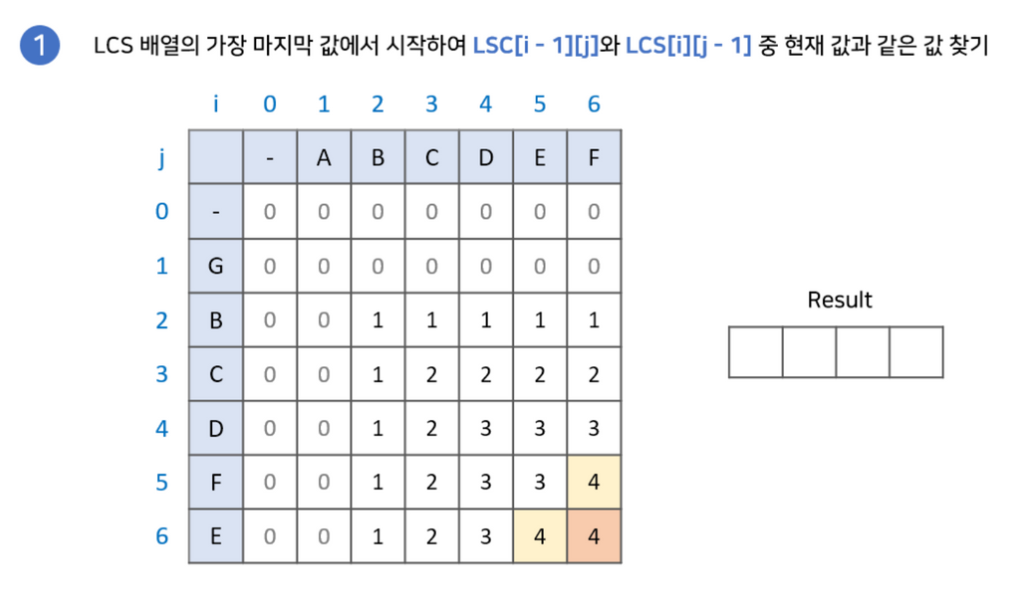
1. LCS 배열의 마지막 값부터 시작합니다. 결과값을 저장한 변수 또한 설정해줍니다.
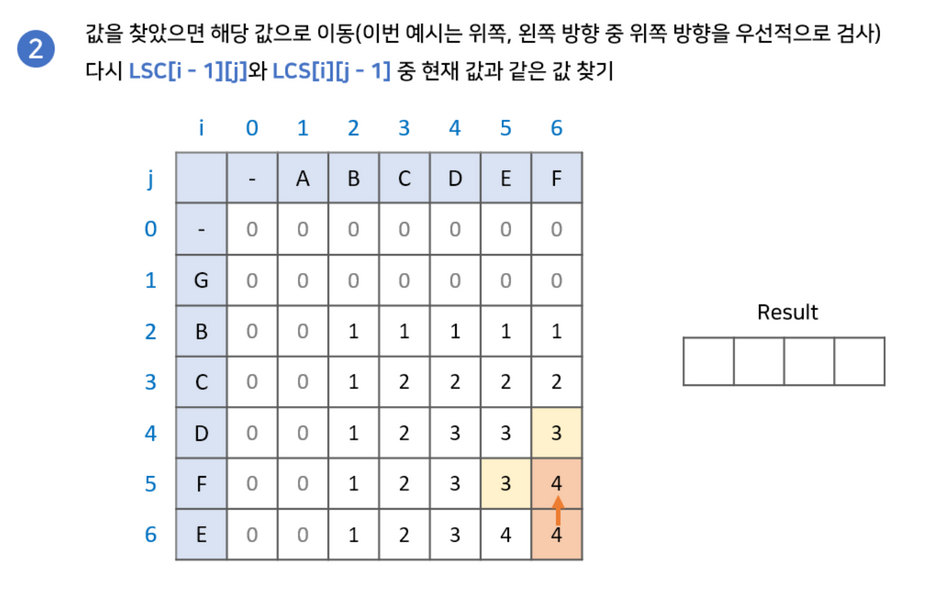
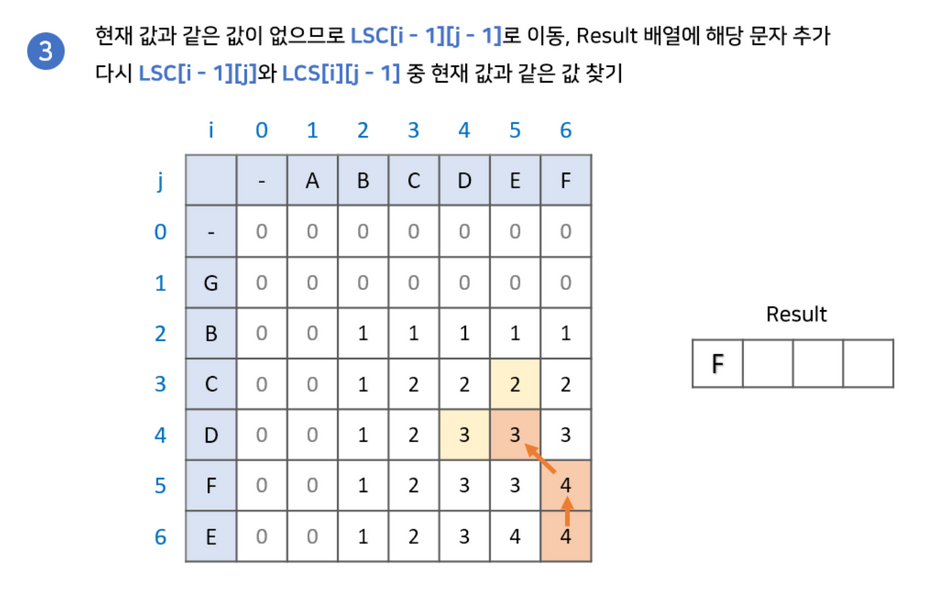
2. LCS[i-1][j]와 LCS[i][j-1] 중 현재 값과 같은 값을 찾습니다.2-2. 만약 없다면 해당 문자를 넣고 LCS[i-1][j-1]로 이동합니다.
3. 2-1. 만약 같은 값이 있다면 해당 값으로 이동합니다.
4. (0,0)으로 이동하기 전까지 2번을 반복해줍니다.

위 식을 반복하여 나온 결과값의 역순이 우리가 구하고자 하는 LCS값입니다.

다음은 구현 과정입니다.

 

 

알고리즘을 풀던 도중 해당 개념을 알고 있어야 풀 수 있는 문제를 만나서 공부하는 김에 정리를 해보았습니다.

 

제가 참고하며 공부했던 블로그에서 매우 자세하게 설명해주고 있어서 해당 링크 또한 남기도록 하겠습니다.

 

https://velog.io/@emplam27/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-LCS-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Longest-Common-Substring%EC%99%80-Longest-Common-Subsequence