누적 합
누적 합이란 수열에 대해 각 인덱스까지의 구간의 합을 구하는 것을 의미합니다.
모든 구간에 대해 단순하게 반복하여 하나씩 더해가는 방법을 사용하게 되면 최악의 경우 O(n^2)의 시간 복잡도를 가질 수 있습니다.
하지만 이전 인덱스까지의 누적합에 현재 값을 더하는 방식인 누적 합을 사용하면 O(n)의 시간 복잡도를 가질 수 있습니다.
배열에 따라 누적합을 저장해놓은 뒤, 구하고자 하는 범위까지의 누적합에서 해당 범위에 포함되지 않는 범위를 빼주면 구할 수 있습니다.
따라서 배열의 특정 범위의 구간 합을 구하고자 한다면, 해당 알고리즘이 매우 유용할 수 있습니다.
예시
백준 11659 문제인 구간 합 구하기 4를 통해 누적합에 대해 알아보겠습니다.
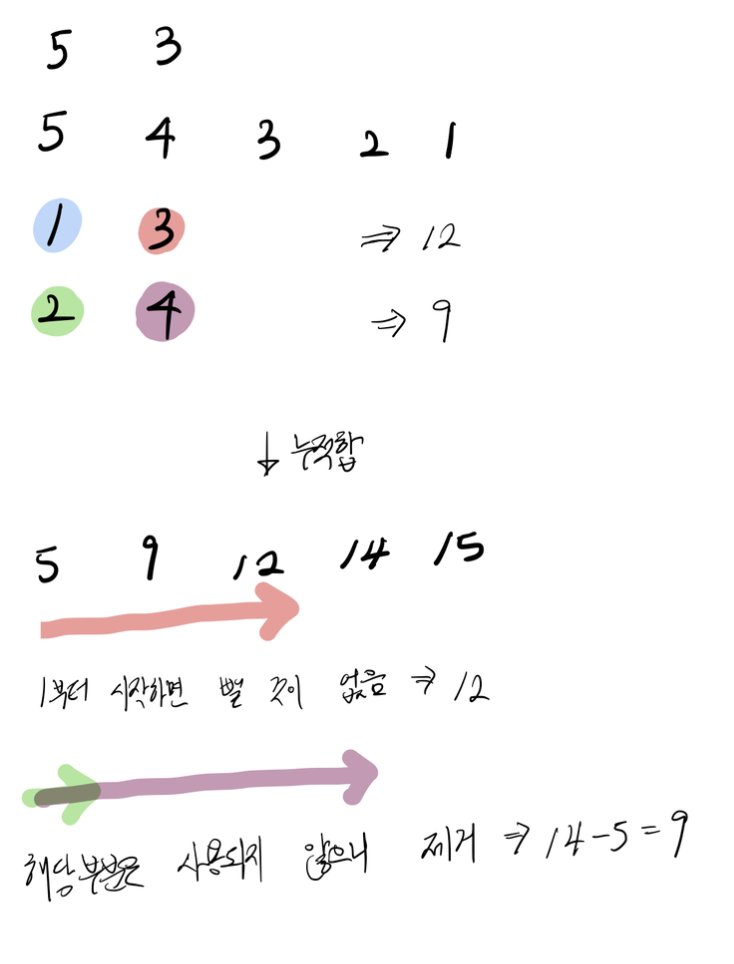
우선 5 4 3 2 1에 대한 누적합을 구하고 배열로 나타낸다면 [5, 9, 12, 14, 15]로 표시할 수 있습니다.
여기서 예를 들어 2 ~ 4번째 숫자에 대한 값을 알고 싶다면, 4번째까지의 누적합에서 1번째까지의 누적합을 빼주면 알 수 있습니다.
그림으로 보면 더욱 이해하기 쉬울 거 같아 그림으로 정리해보았습니다.
728x90
'CS > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [알고리즘] 슬라이딩 윈도우(Sliding Window) (0) | 2023.09.01 |
|---|---|
| [알고리즘] 투 포인터(Two Pointer) (0) | 2023.09.01 |
| [알고리즘] 메모이제이션(Memoization) (0) | 2023.08.18 |
| [알고리즘] LCS (0) | 2023.08.14 |
