[Silver III] 2×n 타일링 - 11726
성능 요약
메모리: 69100 KB, 시간: 12 ms
분류
다이나믹 프로그래밍
제출 일자
2024년 1월 29일 14:49:07
문제 설명
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

입력
첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
출력
첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
풀이
해당 문제를 풀기 위해서 "순열"을 떠올릴 필요가 있습니다.
예를 들어 [1, 2, 3, 4]라는 숫자들의 조합을 나타내는 방법은 4! = 24입니다. 여기서 만약 첫 번째 자리를 1로 고정한다면
숫자들의 조합은 (4-1)! = 6이 될 것입니다. 이 개념을 기억하고 있으면 해당 문제를 푸는 데에 있어 용이하기 때문에 설명하였습니다.
우선 식의 규칙을 찾기 위해 하나씩 대입해보았습니다.
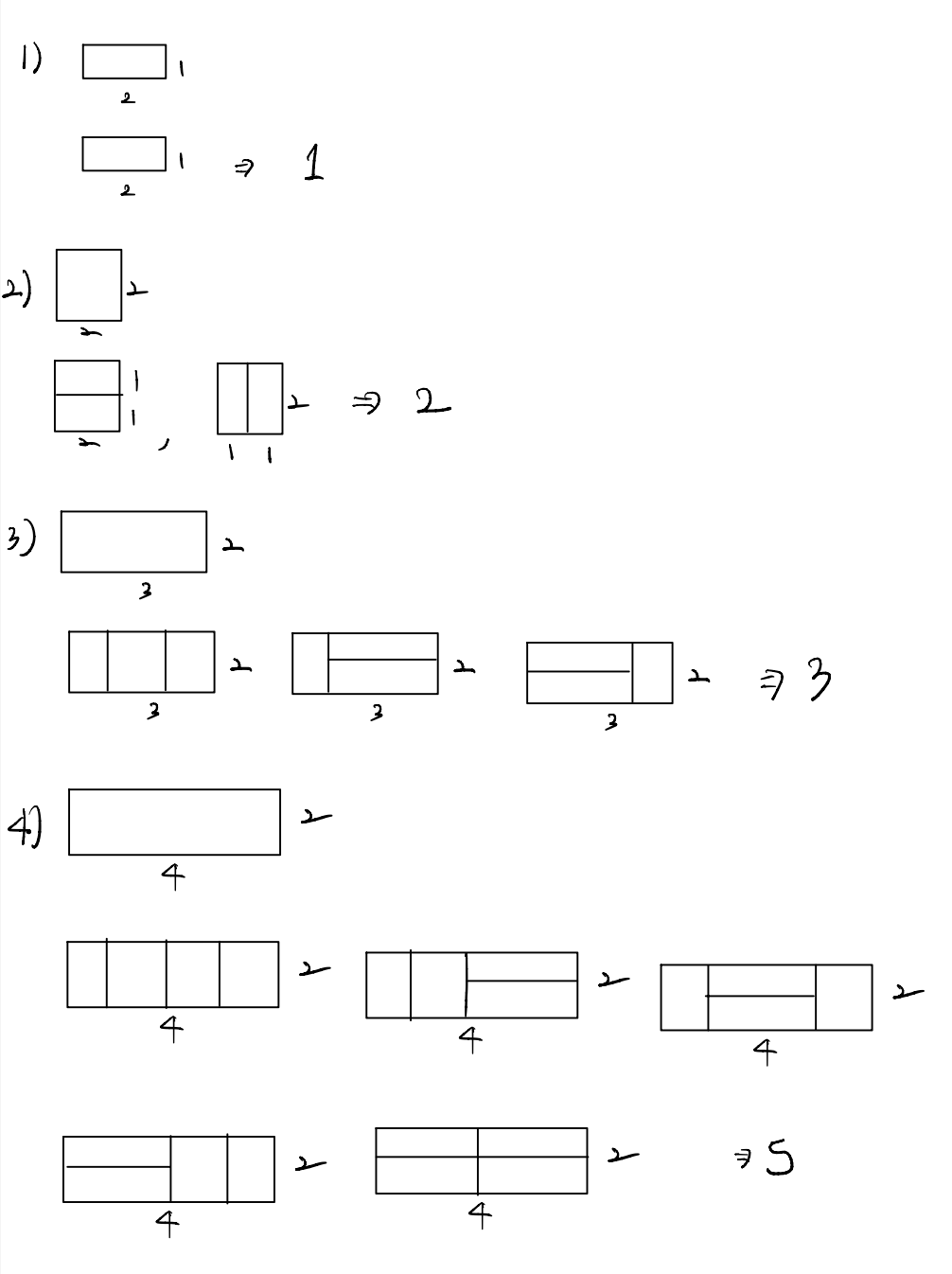
DP에서 가장 중요한 점은 이전에 계산한 것을 어떻게 활용하는 지가 중요하다고 생각했습니다.
우선 N이 3이 되었을 때 N이 2일 때와 비교해본다면, 한 자리를 고정시켜두면 2 x 2를 구하는 것과 같음을 알 수 있습니다.
이는 dp[N-1]이 될 것입니다.
또한 두 자리를 고정한다고 한다면 1 x 2를 구하는 것과 같은데, 이는 dp[N-2]입니다.
왜냐하면 지금은 N이 3일 때까지라서 보이진 않는데, 만약 N의 값이 더욱 커진다면, 두 자리를 고정하는 것도 생각해야 하기 때문에 구해주었습니다.
위의 식을 보면 N이 4일 때, 한 자리를 |로 고정하고 3 x 2를 구하는 것과 두 자리를 =로 고정하고 2 x 2를 구해야 총 구하는 개수이기 때문입니다.
여기서 N-2까지만 하는 이유는 사실 N-3은 N-2와 N-1의 조합으로 나타낼 수 있기 때문에 dp[N] = dp[N-2] + dp[N-1]을 통해 답을 유추할 수 있습니다.
다음은 코드입니다.
let n = Int(readLine()!)!
var dp = [Int](repeating: 0, count: 1001)
(dp[1], dp[2]) = (1, 2)
if n <= 2 {
print(dp[n])
} else { // n이 3이상일 때
for i in 3...n {
dp[i] = dp[i - 2] + dp[i - 1]
if dp[i] >= 10007 {
dp[i] %= 10007
}
}
print(dp[n])
}
'PS > BOJ' 카테고리의 다른 글
| [백준(BOJ)] 9655 돌 게임 - 스위프트 (Swift) (0) | 2024.02.18 |
|---|---|
| [백준(BOJ)] 1912 연속합 - 스위프트 (Swift) (2) | 2024.02.18 |
| [백준(BOJ)] 9024 두 수의 합 - 스위프트 (Swift) (2) | 2024.01.21 |
| [백준(BOJ)] 17951 흩날리는 시험지 속에서 내 평점이 느껴진거야 - 스위프트 (Swift) (2) | 2024.01.21 |
| [백준(BOJ)] 16401 과자 나눠주기 - 스위프트 (Swift) (0) | 2024.01.21 |
