[백준 (BOJ)] 2590 색종이 - 스위프트(Swift)
[Gold IV] 색종이 - 2590
성능 요약
메모리: 69100 KB, 시간: 12 ms
분류
많은 조건 분기, 그리디 알고리즘
제출 일자
2023년 11월 7일 13:40:40
문제 설명
<그림 1>과 같이 정사각형 모양을 한 여섯 종류의 색종이가 있다. 1번 색종이는 한 변의 길이가 1cm이고, 차례대로 그 길이가 1cm씩 커져, 6번 색종이의 한 변의 길이는 6cm가 된다.
<그림 1>
주어진 색종이를 <그림 2>와 같이 가로, 세로의 길이가 각각 6cm인 판 위에 붙이려고 한다. 색종이를 붙일 때는 색종이가 판의 경계 밖으로 삐져 나가서는 안되며, 색종이가 서로 겹쳐서도 안 된다. 또한 하나의 색종이는 하나의 판에만 붙여야 한다.
<그림 2>
각 종류별로 색종이의 장수가 주어질 때, 그 색종이를 모두 붙이기 위해서 위와 같은 판이 최소 몇 개가 필요한지 구하는 프로그램을 작성하시오.
입력
첫째 줄부터 여섯째 줄까지 각 종류의 색종이의 장수가 1번부터 6번까지 차례로 주어진다. 각 종류의 색종이의 장수는 최대 100이다.
출력
첫째 줄에 필요한 판의 최소 개수를 출력한다.
풀이
우선 큰 색종이부터 채워나가면서, 남은 공간에 색종이를 추가적으로 넣을 수 있다면 넣는 방식을 생각했습니다.
(그런데 처음에 문제를 제대로 읽지 않아서 색종이를 붙일 때는 색종이가 판의 경계 밖으로 삐져 나가서는 안되며, 색종이가 서로 겹쳐서도 안 된다. 또한 하나의 색종이는 하나의 판에만 붙여야 한다.의 문장을 보지 못해 조금 헤맸습니다,, 문제를 잘 읽읍시다!)
1. 우선 6x6 색종이는 하나를 다 차지하기 때문에 색종이의 개수만큼 판이 필요합니다.
2. 5x5 색종이를 붙인 뒤에는 1x1 색종이를 11장까지 붙일 수 있습니다.
3. 4x4 색종이를 붙인 뒤에는 2x2 색종이를 5장까지 붙이거나, 나머지는 1x1 색종이를 붙일 수 있습니다.
4. 3x3 색종이 같은 경우에는 4개까지 붙일 수 있어, 만약 4장 이상이라면 4개를 채우고,
3개라면 2x2 색종이를 1장까지 붙일 수 있고, 2개라면 2x2 색종이를 3장, 1개라면 2x2 색종이를 5장까지 붙일 수 있습니다.
5. 2x2 색종이는 최대 9장까지 붙일 수 있고, 나머지는 1x1 색종이를 붙일 수 있습니다.
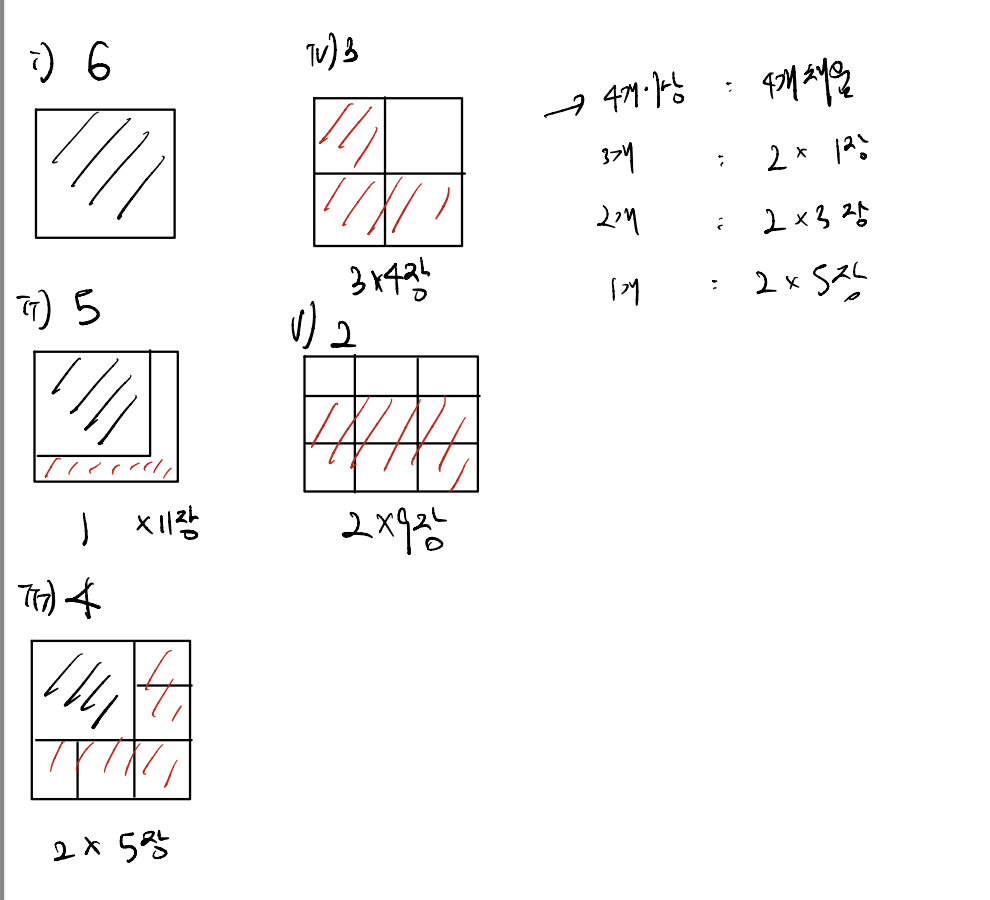
위의 규칙을 기준으로 가장 큰 6x6 색종이부터 해당 색종이가 없어질 때까지 판의 개수를 구하면 됩니다.
다음은 코드입니다.
var paper = [0]
var ans = 0
for _ in 0..<6 {
if let input = readLine(), let value = Int(input) {
paper.append(value)
}
}
if paper[6] > 0 {
ans += paper[6]
}
while paper[5] > 0 {
let area = 36 - 5 * 5
paper[5] -= 1
paper[1] = max(paper[1] - area, 0) // 나머지는 1로 채움
ans += 1
}
while paper[4] > 0 {
var area = 36 - 4 * 4
area -= min(paper[2], 5) * 4 // 2로 최대 5개까지 채움
paper[4] -= 1
paper[2] = max(paper[2] - 5, 0) // 나머지는 2로 채움
paper[1] = max(paper[1] - area, 0) // 남는 공간 1로 채움
ans += 1
}
while paper[3] > 0 {
var area = 36 - 9 * min(paper[3], 4)
if paper[3] >= 4 { // 4개 이상이면 4개를 채움
paper[3] -= 4
area = 0
} else if paper[3] == 3 { // 3개면 2를 최대 한 장 채움
area -= min(1, paper[2]) * 4
paper[3] -= 3
paper[2] = max(paper[2] - 1, 0)
} else if paper[3] == 2 { // 2개면 2를 최대 3개 채움
area -= min(3, paper[2]) * 4
paper[3] -= 2
paper[2] = max(paper[2] - 3, 0)
} else { // 1개면 2를 최대 5개 채움
area -= min(5, paper[2]) * 4
paper[3] -= 1
paper[2] = max(paper[2] - 5, 0)
}
paper[1] = max(paper[1] - area, 0)
ans += 1
}
while paper[2] > 0 {
let area = 36 - 4 * min(paper[2], 9)
paper[2] = max(paper[2] - 9, 0)
paper[1] = max(paper[1] - area, 0) // 2로 채우고 나머지를 1로 채움
ans += 1
}
while paper[1] > 0 {
paper[1] = max(paper[1] - 36, 0)
ans += 1
}
print(ans)